randomForestSRC Algorithm

Hemant Ishwaran

Min Lu

Udaya B. Kogalur

2023-05-29

General Description of the RF algorithm

The random forest algorithm can be broadly described as follows:

  1. Draw ntree bootstrap samples from the original data.

  2. Grow a tree for each bootstrapped dataset. At each node of the tree randomly select mtry variables for splitting on. Split on the variable that optimizes a chosen splitting criterion.

  3. Grow the tree to full size under the constraint that a terminal node should have no less than nodesize unique cases. Calculate the tree predictor.

  4. Calculate in-bag and out-of-bag (OOB) ensemble estimators by averaging the tree predictors.

  5. Use the OOB estimator to estimate out-of-sample prediction

  6. Use OOB estimation to calculate variable importance.

Recursive Algorithm

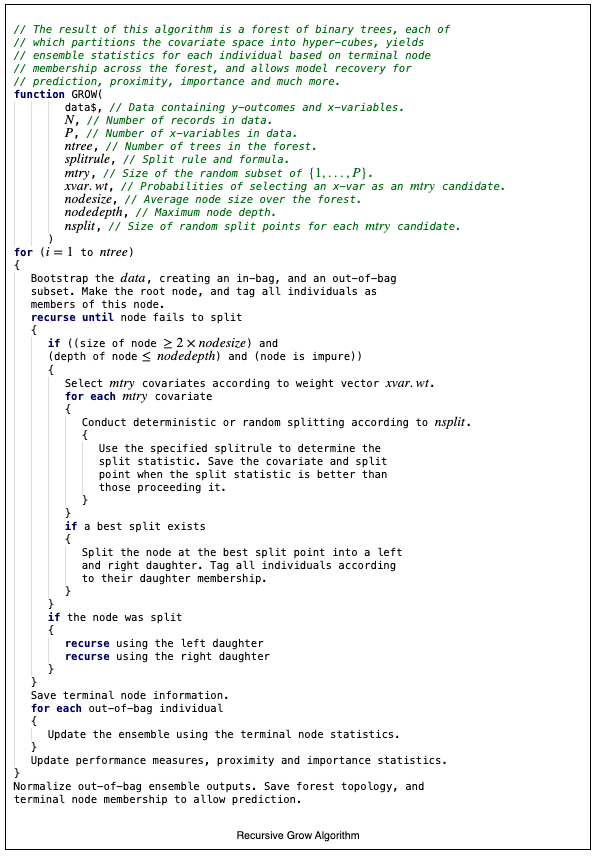
The basic algorithm for growing a forest is provided in the recursive algorithm provided below:

The process iterates over ntree, the number of trees that are to be grown. In practice, the iteration is actually parallelized and trees are grown concurrently, not iteratively. This is explained in more detail in the vignette on Hybrid Parallel Processing [1]. The recursive nature of the algorithm is reflected in the repeated calls to split a node until conditions determine that a node is terminal. Another key aspect of the algorithm is the injection of randomization during model creation. Randomization reduces variation. Bootstrapping [2] at the root node reduces variation. Feature selection is also randomized with the use of the parameter mtry. In the Recursive Algorithm N is defined as the number of records in the data set, and P as the number of \(X\)-variables in the data set. The parameter mtry is such that \(1\le\) mtry \(\le P\). At each node, the algorithm selects mtry random \(X\)-variables according to a probability vector xvar.wt. The resulting subset of \(X\)-variables are examined for best splits according to a splitrule. The parameter nsplit also allows one to specify the number of random split points at which an \(X\)-variable is tested. The depth of trees can be controlled using the parameters nodesize and nodedepth. The parameter nodesize ensures that the average nodesize across the forest will be at least nodesize. The parameter nodedepth forces the termination of splitting when the depth of a node reaches the value specified. Node depth is zero-based from the root node onward. Reasonable models can be formed with the judicious selection of mtry, nsplit, nodesize, and nodedepth without exhaustive and deterministic splitting.

Recursive Algorithm



Cite this vignette as
H. Ishwaran, M. Lu, and U. B. Kogalur. 2021. “randomForestSRC: randomForestSRC algorithm vignette.” http://randomforestsrc.org/articles/algorithm.html. 

@misc{HemantAlgorithm,
    author = "Hemant Ishwaran and Min Lu and Udaya B. Kogalur",
    title = {{randomForestSRC}: {randomForestSRC} algorithm vignette},
    year = {2021},
    url = {http://randomforestsrc.org/articles/algorithm.html},
    howpublished = "\url{http://randomforestsrc.org/articles/algorithm.html}",
    note = "[accessed date]"
}

References

1. Ishwaran H, Lu M, Kogalur UB. randomForestSRC: Hybrid parallel processing vignette. 2021. http://randomforestsrc.org/articles/hybrid.html.
2. Breiman L. Bagging predictors. Machine learning. 1996;24:123–40.